LLVM 週期術語

週期

週期是 LLVM 迴圈 的一般化，遞迴定義如下 [HavlakCycles]

  1. 在有向圖 G 中，若 G 是函數 CFG 或其子圖，則週期是一個極大的強連通區域，且至少有一條內部邊。（資訊性註記 — 至少一條內部邊的要求確保只有當存在返回同一基本區塊的邊時，單一基本區塊才是一個週期。）

  2. 週期中的一個基本區塊，若可以從函數的入口沿著不訪問週期中任何其他基本區塊的路徑到達，則稱為該週期的入口。一個週期可以有多個入口。

  3. 對於從函數入口開始給定的深度優先搜尋，週期中第一個被訪問的節點稱為相對於此特定 DFS 的此週期的標頭。標頭始終是一個入口節點。

  4. 在任何從入口開始的深度優先搜尋中，在 CFG 中找到的週期集合是相同的。這些是不具有父週期的頂層週期。

  5. 巢狀在以標頭 H 的週期 C 內部的子週期（或簡稱週期）是在節點集合 (C - H) 上誘導的子圖中的週期。C 被稱為這些週期的父週期。

因此，週期形成一個實作定義的森林，其中每個週期 C 是巢狀在 C 內部的任何子週期的父週期。樹狀結構緊密地遵循相同函數中迴圈的巢狀結構。可歸約週期（LLVM 迴圈）L 的唯一入口支配其所有其他節點，並且始終被選為某個週期 C 的標頭，而與使用的 DFS 樹無關。此週期 C 是迴圈 L 的超集。對於不可歸約週期，沒有一個入口支配週期的節點。其中一個入口以實作定義的方式被選為週期的標頭。

如果一個週期有多個入口，則它是不可歸約的，否則它是可歸約的。

如果基本區塊 B 出現在週期 C 中，但未出現在 C 的任何子週期中，則稱週期 C 是基本區塊 B 的父週期。然後 B 也被稱為週期 C 的子週期。

如果區塊 B 不是任何週期的子週期，則稱區塊 B 為頂層區塊。

如果基本區塊或週期 X 與另一個基本區塊或週期 Y 都沒有父週期，或者兩者都具有相同的父週期，則它們是同級。

資訊性註記

  • 週期的非標頭入口區塊可以包含在子週期中。

  • 如果 CFG 是可歸約的，則週期正好是自然迴圈，並且每個週期都恰好有一個入口區塊。

  • 週期是良好巢狀的（根據定義）。

  • 週期的入口區塊在支配樹中是同級的。

[HavlakCycles]

Paul Havlak, “可歸約和不可歸約迴圈的巢狀結構。” ACM Transactions on Programming Languages and Systems (TOPLAS) 19.4 (1997): 557-567。

週期的範例

包圍自然迴圈的不可歸約週期

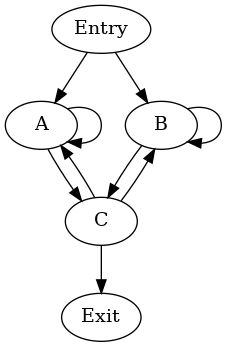
_images/cycle-1.png

A 和 B 的自迴圈產生兩個單區塊自然迴圈。可能的週期層次結構是

cycle: {A, B, C} entries: {A, B} header: A
- cycle: {B, C}  entries: {B, C} header: C
  - cycle: {B}   entries: {B}    header: B

當 DFS 以 A、C、B 的順序（前序）訪問區塊時，會出現此層次結構。

兩個自然迴圈的不可歸約聯集

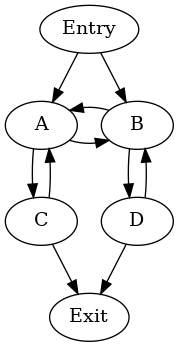
_images/cycle-2.png

有兩個自然迴圈：{A, C} 和 {B, D}。可能的週期層次結構是

cycle: {A, B, C, D} entries: {A, B} header: A
- cycle: {B, D}     entries: {B}    header: B

沒有自然迴圈的不可歸約週期

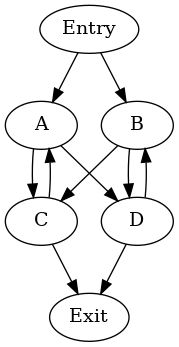
_images/cycle-3.png

此圖不包含任何自然迴圈 — 節點 A、B、C 和 D 在支配樹中是同級的。可能的週期層次結構是

cycle: {A, B, C, D} entries: {A, B} header: A
- cycle: {B, D}     entries: {B, D} header: D

封閉路徑與週期

CFG 中的封閉路徑是 CFG 中節點和邊的連通序列，其起始節點和結束節點相同，且其餘（內部）節點是不同的。

封閉路徑 P 的入口是 P 上的一個節點，可以從函數入口到達，而無需通過 P 上的任何其他節點。

  1. 如果節點 D 支配封閉路徑 P 中的一個或多個節點，且 P 不包含 D，則 D 支配 P 中的每個節點。

    證明： 令 U 為 P 中受 D 支配的節點。如果 P 中存在不受 D 支配的節點 V，則 U 可以從函數入口節點經由 V 到達，而無需通過 D，這與 D 支配 U 的事實相矛盾。

  2. 如果節點 D 支配封閉路徑 P 中的一個或多個節點，且 P 不包含 D，則存在一個週期 C，其包含 P 但不包含 D。

    證明： 從上述屬性，D 支配 P 中的所有節點。對於實作定義的 DFS 發現的任何週期巢狀結構，考慮包含 P 的最小週期 C。為了反證，假設 D 在 C 中。那麼 C 的標頭 H 不能在 P 中，因為週期的標頭不能被週期中的任何其他節點支配。因此，P 在集合 (C-H) 中，並且在 C 中必定存在一個也包含 P 的較小週期 C'，這與我們選擇 C 的方式相矛盾。

  3. 如果封閉路徑 P 包含節點 U1 和 U2，但不包含它們的支配者 D1 和 D2，則存在一個週期 C，其包含 U1 和 U2，但不包含 D1 和 D2 中的任何一個。

    證明： 從上述屬性，每個 D1 和 D2 分別支配 P 中的每個節點。存在一個週期 C1（分別為 C2），其包含 P 但不包含 D1（分別為 D2）。C1 和 C2 要么是同一個週期，要么其中一個巢狀在另一個內部。因此，始終存在一個週期，其包含 U1 和 U2，但不包含 D1 和 D2 中的任何一個。

  1. 在任何週期層次結構中，包含封閉路徑 P 的最小週期 C 的標頭 H 本身位於 P 上。

    證明： 如果 H 不在 P 中，則在集合 C - H 中存在一個包含 P 的較小週期 C'，因此與 C 是最小此類週期的聲明相矛盾。

可歸約週期標頭

儘管週期層次結構取決於選擇的 DFS，但可歸約週期滿足以下不變性

如果在任何 DFS 中發現標頭為 H 的可歸約週期 C，則在每個標頭為 H 的 DFS 中都存在一個週期 C'，其包含 C。

證明： 對於 C 中通過 H 的封閉路徑 P，每個週期層次結構都有一個包含 P 且其標頭在 P 中的最小週期 C'。由於 H 是 P 的唯一入口，因此 H 必定是 C' 的標頭。由於標頭唯一地定義了週期，因此 C' 包含每個這樣的封閉路徑 P，因此 C' 包含 C。