收斂與一致性¶
簡介¶
在某些環境中,執行緒群組並行執行相同的程式,其中使用稱為收斂操作的特殊原語建立群組內的有效通訊。收斂操作的結果對參與其中的執行緒集合很敏感。
收斂的直觀圖像圍繞著以「鎖步」方式執行的執行緒建立——一組執行緒被認為是收斂的,如果它們都在「一起執行相同的指令序列」。這些執行緒可能會在發散分支處發散,並且它們可能會在稍後在某些共同的程式點重新收斂。
在這個直觀的圖像中,當收斂的執行緒執行指令時,如果結果值在這些執行緒中是相同的,則稱其為一致的,否則為發散的。 相應地,如果分支的條件是一致的,則稱分支為一致分支,否則為發散分支。
但是,鎖步執行的假設對於描述收斂操作的通訊並非必要。 它也透過過度指定執行緒在這種並行環境中如何執行來約束實作(編譯器以及硬體)。 為了消除這個假設
我們將收斂定義為不同執行緒執行每個指令之間的關係,而不是執行緒本身之間的關係。 這個定義對於已知的目標是合理的,並且與 LLVM IR 中收斂操作的語義相容。
我們也根據這種收斂性定義一致性。 只有在指令的相應執行是收斂的情況下,才能檢查指令的輸出在多個執行緒之間的一致性。
本文檔描述了一個靜態分析,用於確定函數中每個指令的收斂性。 該分析擴展了先前關於發散分析的工作[DivergenceSPMD]以涵蓋不可簡化的控制流程。 所描述的分析用於 LLVM 中,以實作 UniformityAnalysis,該分析確定 LLVM IR 或 MIR 函數中每個指令計算的值的一致性。
Julian Rosemann, Simon Moll, 和 Sebastian Hack。 2021 年。用於可簡化控制流程圖的 SPMD 發散的抽象解釋。 Proc. ACM Program. Lang. 5, POPL, Article 31 (2021 年 1 月), 35 頁。 https://doi.org/10.1145/3434312
動機¶
發散分支約束了程式轉換,例如更改 CFG 或將收斂操作移動到 CFG 的不同點。 跨發散分支執行這些轉換可能會更改以收斂方式執行收斂操作的執行緒集合。 雖然這些約束不在本文檔的範圍內,但一致性分析允許這些轉換識別這些約束不成立的一致分支。
一致性本身也適用於在群組中執行執行緒並共享執行資源的目標(例如 waves、warps 或 subgroups)
一致的輸出可能可以計算或儲存在共享資源上。
這些目標必須「線性化」發散分支,以確保分支的每一側都由同一群組中的相應執行緒遵循。 但是,在一致分支中,線性化是不必要的,因為整個執行緒群組要么遵循分支的一側,要么遵循另一側。
術語¶
執行緒與動態實例¶
程式原始碼中指令的每次出現都稱為靜態實例。 當執行緒執行程式時,靜態實例的每次執行都會產生該指令的不同動態實例。
每個執行緒產生一個唯一的動態實例序列
該序列是沿分支決策和迴圈遍歷產生的。
從「第一個」指令的動態實例開始。
繼續使用後續「下一個」指令的動態實例。
執行緒是獨立的; 某些目標可能會選擇以群組方式執行它們,以便在可能的情況下共享資源。
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||
執行緒 1 |
進入1 |
H1 |
B1 |
L1 |
H3 |
L3 |
退出 |
||||
執行緒 2 |
進入1 |
H2 |
L2 |
H4 |
B2 |
L4 |
H5 |
B3 |
L5 |
退出 |
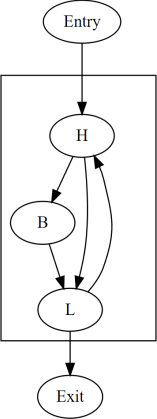
在上表中,每一行是一個不同的執行緒,從左到右列出該執行緒產生的動態實例。 每個執行緒都執行相同的程式,該程式以 Entry 節點開始,並以 Exit 節點結束,但不同的執行緒可能會採用程式控制流程中的不同路徑。 列的編號僅為了方便起見,空單元格沒有特殊含義。 同一列中列出的動態實例是收斂的。
收斂¶
先於收斂是動態實例上的嚴格偏序關係,定義為以下各項的傳遞閉包
如果動態實例
P在同一個執行緒中嚴格先於Q執行,則P先於收斂Q。如果動態實例
P在同一個執行緒中嚴格先於Q1執行,且Q1與Q2收斂,則P先於收斂Q2。如果動態實例
P1與P2收斂,且P2在同一個執行緒中嚴格先於Q執行,則P1先於收斂Q。
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
執行緒 1 |
進入 |
… |
S2 |
T |
… |
退出 |
|||
執行緒 2 |
進入 |
… |
Q2 |
R |
S1 |
… |
退出 |
||
執行緒 3 |
進入 |
… |
P |
Q1 |
… |
上表顯示了來自不同執行緒的動態實例的部分序列。 同一列中的動態實例被假定為收斂的(即,在收斂關係中彼此相關)。 結果收斂順序包括邊 P -> Q2、Q1 -> R、P -> R、P -> T 等。
與...收斂是不同執行緒為同一靜態實例產生的動態實例上的傳遞對稱關係。
為與...收斂關係提供任何一個定義是不切實際的,因為不同的環境可能希望以不同的方式關聯動態實例。 先於收斂是嚴格偏序關係,這是對與...收斂關係的約束。 如果不同的動態實例永遠不收斂,則很容易滿足此條件。 下面,我們提供一個稱為最大與...收斂的關係,它滿足先於收斂,並且適用於已知的目標。
注意
先於收斂關係不是直接可觀察的。 程式轉換通常可以自由更改指令的順序,即使這顯然會更改先於收斂關係。
收斂的動態實例不需要同時執行,甚至不需要在相同的資源上執行。 收斂操作的收斂動態實例可能看起來是這樣做的,但這是一個實作細節。
P先於收斂Q的事實並不自動意味著P在記憶體模型意義上先於發生Q。
最大收斂¶
本節定義了一個約束,可用於產生最大與...收斂關係,而不會違反嚴格的先於收斂順序。 這種最大與...收斂關係對於真實目標是合理的,並且與收斂操作相容。
最大與...收斂關係是根據循環標頭定義的,並假設執行緒在循環的每次「迭代」中在標頭處收斂。 非正式地說,如果兩個執行緒在進入該循環後都先前執行了循環標頭相同次數,則它們執行循環的相同迭代。 一般來說,這也需要考慮父循環的迭代。
最大與...收斂
如果且僅當滿足以下條件時,不同執行緒為同一靜態實例
X產生的動態實例X1和X2在最大與...收斂關係中收斂
X不包含在任何循環中,或者,對於每個包含
X且標頭為H的循環C
在相應執行緒中先於
X1的每個H的動態實例H1都先於收斂X2,並且,在相應執行緒中先於
X2的每個H的動態實例H2都先於收斂X1,不假設
X1與X2收斂。
注意
如果 CFG 是不可簡化的,則循環標頭對於給定的 CFG 可能不是唯一的。 同一個 CFG 的每個循環層次結構都會導致不同的最大與...收斂關係。
為簡潔起見,本文檔的其餘部分將術語收斂限制為表示「在給定循環層次結構的最大與...收斂關係下相關」。
現在可以在先前的範例中示範最大收斂,如下所示
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||
執行緒 1 |
進入1 |
H1 |
B1 |
L1 |
H3 |
L3 |
退出 |
||||
執行緒 2 |
進入2 |
H2 |
L2 |
H4 |
B2 |
L4 |
H5 |
B3 |
L5 |
退出 |
Entry1和Entry2是收斂的。H1和H2是收斂的。B1和B2由於H4而未收斂,H4不是先於收斂B1。H3和H4是收斂的。H3由於H4而未與H5收斂,H4不是先於收斂H3。L1和L2是收斂的。L3和L4是收斂的。L3由於H5而未與L5收斂,H5不是先於收斂L3。
對循環標頭的依賴¶
先於收斂中的矛盾僅可能發生在位於某個循環內部的兩個節點之間。 這些節點的動態實例可能會在同一個執行緒中交錯,並且這種交錯對於不同的執行緒可能會有所不同。 循環標頭充當最大與...收斂關係中的隱式收斂點。 當執行緒執行節點 X 一次,然後再次執行它時,它必定遵循了 CFG 中包含 X 的封閉路徑。 這樣的路徑必須通過至少一個循環的標頭——包含整個封閉路徑的最小循環。 在給定的執行緒中,X 的兩個動態實例要么被至少一個循環標頭的執行分隔開,要么 X 本身就是一個循環標頭。
考慮一系列巢狀循環 C1、C2、…、Ck,其中 C1 是最外層的循環,Ck 是最內層的循環,標頭分別為 H1、H2、…、Hk。 當執行緒進入循環 Ck 時,以下任何一種情況都是可能的
執行緒直接進入循環
Ck,而沒有執行任何標頭H1到Hk中的任何一個。執行緒執行了一些或所有巢狀標頭一次或多次。
最大與...收斂關係捕捉了關於循環的以下直覺
當兩個執行緒進入頂層循環
C1時,它們執行每個節點的收斂動態實例,這些節點是 C1 的子項。當兩個執行緒進入巢狀循環
Ck時,它們執行每個節點的收斂動態實例,這些節點是Ck的子項,直到任一執行緒退出Ck,當且僅當它們執行了任一執行緒遇到的最後一個巢狀標頭的收斂動態實例時。請注意,當執行緒退出巢狀循環
Ck時,它必須遵循Ck外部的封閉路徑才能重新進入它。 這需要執行某個外部循環的標頭,如前所述。
考慮由執行緒 T1 和 T2 為節點 X 產生的兩個動態實例 X1 和 X2,節點 X 是巢狀循環 Ck 的子項。 最大收斂按如下方式關聯 X1 和 X2
如果兩個執行緒都沒有執行任何來自
H1到Hk的標頭,則X1和X2是收斂的。否則,如果沒有任何標頭
H1到Hk(其中Q可能與X相同)的任何收斂動態實例Q1和Q2,使得Q1先於X1且Q2先於X2在各自的執行緒中,則X1和X2不收斂。否則,考慮一對
Q1和Q2,它們是標頭H1到Hk中的標頭Q的收斂動態實例,這些實例在各自的執行緒中最近發生在X1和X2之前。 然後,如果且僅當在執行緒T1中Q1和X1之間,或在執行緒T2中Q2和X2之間,沒有任何來自H1到Hk的標頭的動態實例發生,則X1和X2收斂。 換句話說,Q1和Q2代表最後的收斂點,在執行X之前沒有執行其他標頭。
範例
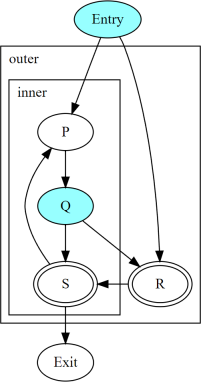
上圖顯示了兩個巢狀不可簡化循環,標頭為 R 和 S。 節點 Entry 和 Q 具有發散分支。 下表顯示了通過 CFG 中不同路徑的三個執行緒之間的收斂性。 同一列中列出的動態實例是收斂的。
1
2
3
4
5
6
7
8
10
執行緒1
進入
P1
Q1
S1
P3
Q3
R1
S2
退出
執行緒2
進入
P2
Q2
R2
S3
退出
執行緒3
進入
R3
S4
退出
P2和P3由於S1而未收斂Q2和Q3由於S1而未收斂S1和S3由於R2而未收斂S1和S4由於R3而未收斂
非正式地說,T1 和 T2 執行內部循環的次數不同,而沒有執行外部循環的標頭。 當所有執行緒首次執行外部循環的標頭時,它們在外部循環中收斂。
一致性¶
如果且僅當兩個收斂動態實例的輸出對於這兩個動態實例比較相等時,它們的輸出才是一致的。
靜態實例
X的輸出對於給定的執行緒集合是一致的,如果且僅當對於這些執行緒產生的X的每對收斂動態實例,它都是一致的。
非一致的值稱為發散的。
對於執行緒的集合 S,靜態實例的每個輸出的一致性確定如下
指令的語義可能會指定輸出是一致的。
否則,如果靜態實例不是m-收斂,則輸出是發散的。
否則,如果靜態實例是 m-收斂的
如果是 PHI 節點,則其輸出是一致的,如果且僅當對於
S中所有執行緒產生的每對收斂動態實例兩個實例都從收斂動態實例中選擇相同的輸出,並且,
該輸出對於
S中的所有執行緒都是一致的。
否則,如果且僅當輸入運算元對於
S中的所有執行緒都是一致的,則輸出才是一致的。
發散循環出口¶
當發散分支發生在循環內部時,發散路徑可能會繼續到循環的出口。 這稱為發散循環出口。 如果循環是不可簡化的,則發散路徑可能會重新進入並最終到達循環內的合併點。 應檢查此類合併點是否符合發散入口標準。
當兩個執行緒在循環內部收斂執行產生一致的值時,但以不同的次數執行標頭後(非正式地說,在循環的不同迭代中)沿著相同的發散路徑退出循環時,位於循環外部的發散路徑上的節點會經歷時間發散。 對於循環內部的節點 N,兩個執行緒的輸出可能是一致的,但循環外部的任何使用 U 都會從 N 的非收斂動態實例接收值。 U 的輸出可能是發散的,具體取決於指令的語義。
靜態一致性分析¶
不可簡化的控制流程會導致不同的循環層次結構,具體取決於深度優先遍歷期間標頭的選擇。 因此,靜態分析並非總是能夠確定不可簡化循環中節點的收斂性,並且任何一致性分析都僅限於那些靜態實例,這些靜態實例的收斂性與循環層次結構無關
m-收斂靜態實例
對於給定的 CFG,如果且僅當靜態實例
X的動態實例的最大與...收斂關係在可以為該 CFG 建構的每個循環層次結構中都相同時,則該靜態實例X是m-收斂的。注意
換句話說,若且唯若 m-收斂靜態實例
X的兩個動態實例X1和X2在某個循環層次結構中是收斂的,則它們對於相同的 CFG 也會在每個其他循環層次結構中收斂。如先前所述,為了簡潔起見,我們將術語收斂限制為表示「在給定循環層次結構中,於最大收斂關係下相關」。
若且唯若包含 X 的每個循環都滿足以下必要條件,則給定 CFG 中的每個節點 X 都會被報告為 m-收斂。
注意
可歸約循環 當然滿足 上述條件。 特別是,如果整個 CFG 是可歸約的,則 CFG 中的所有節點都是 m-收斂的。
靜態實例的每個輸出的均勻性是使用 先前描述的 準則來確定的。 發散輸出的發現可能會導致它們的用途(包括分支)也變得發散。 該分析會傳播這種發散,直到達到不動點。
使用這些準則推斷出的收斂性是任何循環層次結構的最大收斂關係的安全子集。 特別是,即使在檢查其他循環層次結構 T' 時未偵測到該事實,也足以確定靜態實例對於給定循環層次結構 T 是否為 m-收斂。
此屬性允許編譯器轉換使用均勻性分析,而不會受到基礎循環分析中 DFS 選擇的影響。 當兩個轉換對相同的 CFG 使用均勻性分析的不同實例時,一個分析實例中的「發散值」結果不能與另一個分析實例中的「均勻值」結果相矛盾。
諸如 SimplifyCFG、CSE 和迴圈轉換之類的通用轉換通常會以改變最大收斂關係的方式來更改程式。 這也表示先前為均勻的值在這種轉換之後可能會變成發散。 均勻性必須在這種轉換之後重新計算。
循環內部的發散分支¶
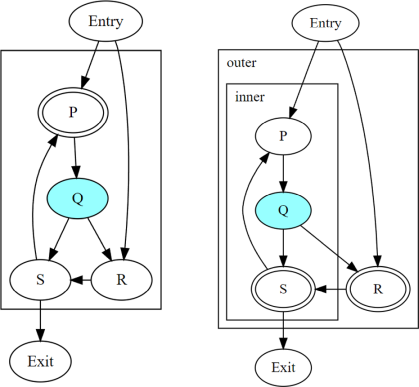
上圖顯示了不可歸約循環區域內部的發散分支 Q。 當兩個執行緒在 Q 處發散時,循環區域內動態實例的收斂性取決於所選擇的循環層次結構。
在偵測到以標頭
P為標頭的單個循環C的實作中,循環內部的收斂性由P決定。在偵測到以標頭
R和S為標頭的兩個巢狀循環的實作中,這些循環內部的收斂性由它們各自的標頭決定。
一種保守的方法是簡單地將不可歸約循環內部的所有節點報告為具有發散輸出。 但是,為了最大化均勻性,期望識別 CFG 中的 m-收斂節點。 本節描述了一種從封閉路徑派生的節點模式,封閉路徑是 CFG 的屬性,不依賴於循環層次結構。
發散進入點準則
只有當對於位於
P上的每個發散分支B及其合併節點J,沒有位於從B到J的發散路徑上的P的進入點時,封閉路徑P中所有節點的動態實例才是 m-收斂的。
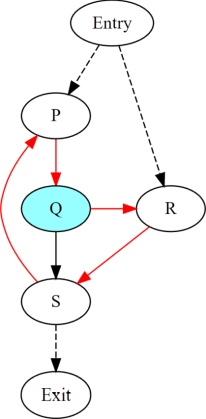
考慮上圖中的封閉路徑 P -> Q -> R -> S。 P 和 R 是 封閉路徑的進入點。 Q 是一個發散分支,而 S 是該分支的合併點,具有發散路徑 Q -> R -> S 和 Q -> S。
如果存在發散進入點
R,則在某些循環層次結構中,R是包含封閉路徑的最小循環C的標頭,並且在集合C - R中存在 子循環C',其中包含分支Q和合併點S。 當執行緒在Q處發散時,一個子集M在循環C'內部繼續執行,而補集N則退出C'並到達R。 由於R的存在,集合M中的執行緒執行的S動態實例與集合N中的執行緒執行的動態實例不收斂。 非正式地說,在Q處發散的執行緒在外部循環C的同一次迭代中重新收斂,但它們可能以不同的方式執行了內部循環C'。1
2
3
4
5
6
7
8
9
10
11
執行緒1
進入
P1
Q1
R1
S1
P3
…
退出
執行緒2
進入
P2
Q2
S2
P4
Q4
R2
S4
退出
在上表中,由於
R1,S2與S1不收斂。
如果
R不存在,或者如果C的標頭是R以外的任何節點,則不會偵測到這樣的子循環C'。 在Q處發散的執行緒執行S的收斂動態實例,因為它們在從Q到S的任何路徑上都沒有遇到循環標頭。 非正式地說,在Q處發散的執行緒在C的同一次迭代中在S處重新收斂。1
2
3
4
5
6
7
8
9
10
執行緒1
進入
P1
Q1
R1
S1
P3
Q3
R3
S3
退出
執行緒2
進入
P2
Q2
S2
P4
Q4
R2
S4
退出
注意
一般來說,上述陳述中的循環
C對於不同的標頭預期不會是同一個循環。 循環及其標頭緊密耦合; 對於同一個最外層循環中的不同標頭,偵測到的子循環可能會有所不同。 與上述範例相關的屬性是,對於每個封閉路徑,都存在一個循環C,其中包含該路徑,且其標頭位於該路徑上。
必須針對每個通過發散分支 B 及其合併點 J 的封閉路徑檢查發散進入點準則。 由於 每個封閉路徑都通過某個循環的標頭,這相當於檢查每個包含 B 和 J 的循環 C。 當 C 的標頭支配合併點 J 時,從標頭到 J 的任何路徑都不可能有進入點,其中包括從 B 到 J 的任何發散路徑。 對於任何通過包含 C 的外部循環標頭的封閉路徑,情況也是如此。
因此,發散進入點準則可以保守地簡化如下:
對於發散分支
B及其合併節點J,僅當滿足以下條件時,包含B和J的循環C中的節點才是 m-收斂的:
B嚴格支配J,或,
C的標頭H嚴格支配J,或,遞迴地,在
C內部存在滿足相同條件的循環C'。
當 J 與 H 或 B 相同時,平凡的支配不足以對發散路徑的進入點做出任何陳述。
到達循環的發散路徑¶
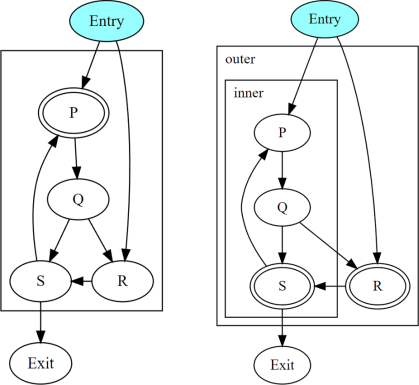
該圖顯示了兩個循環層次結構,其中發散分支位於 Entry 而不是 Q 中。 對於分別在 P 和 R 處進入封閉路徑 P -> Q -> R -> S 的兩個執行緒,沿路徑生成的動態實例的收斂性取決於 P 或 R 是否為標頭。
當
P是標頭時的收斂性。1
2
3
4
5
6
7
8
9
10
11
12
13
執行緒1
進入
P1
Q1
R1
S1
P3
Q3
S3
退出
執行緒2
進入
R2
S2
P2
Q2
S2
P4
Q4
R3
S4
退出
當
R是標頭時的收斂性。1
2
3
4
5
6
7
8
9
10
11
12
執行緒1
進入
P1
Q1
R1
S1
P3
Q3
S3
退出
執行緒2
進入
R2
S2
P2
Q2
S2
P4
…
退出
因此,當發散路徑從循環外部到達不可歸約循環的不同進入點時,靜態分析會保守地將循環中的每個節點報告為非 m-收斂。
可歸約循環¶
如果 C 是標頭為 H 的可歸約循環,則在任何 DFS 中,H 必定是包含 C 的某個循環 C' 的標頭。 與 DFS 無關,除了 H 本身之外,沒有到子圖 C 的進入點。 因此,我們有以下結論:
對於發散分支及其合併點(兩者都在子圖
C內部),發散進入點準則當然滿足。當發散路徑從外部到達子圖
C時,它們的收斂性始終由同一個標頭H決定。
顯然,這只能在循環層次結構 T 中確定,其中 C 被偵測為可歸約循環。 在不同的循環層次結構 T' 中無法得出這樣的結論,其中 C 是具有相同標頭的較大循環 C' 的一部分,但這與 T 中的結論並不矛盾。
受控收斂¶
收斂控制權杖 為確定哪些執行緒在程式中的給定點收斂提供了明確的語義。 其影響被納入動態實例上的 受控最大收斂關係 和靜態實例的 受控 m-收斂 屬性中。 LLVM 中實作的 均勻性分析 針對支援收斂控制權杖的目標包含了這一點。
